What is a JFET transistor and how it works

This post is about structure, parameters and properties of JFET transistor.

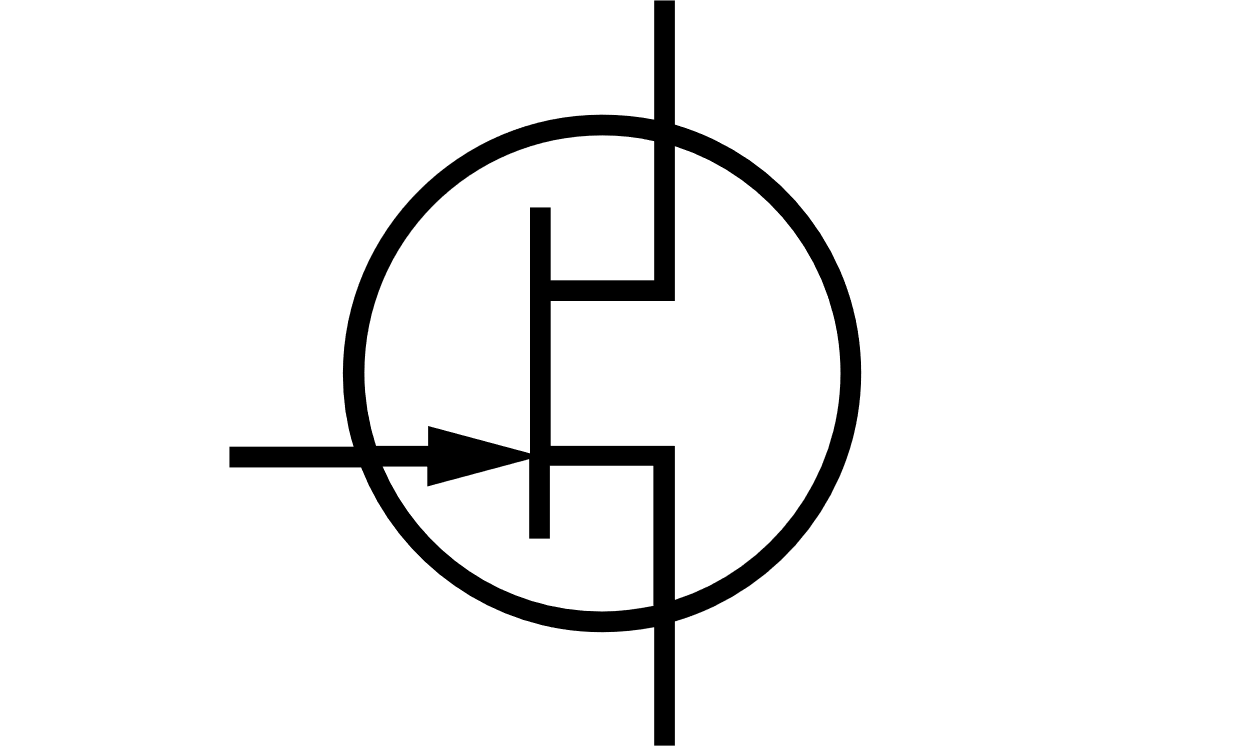
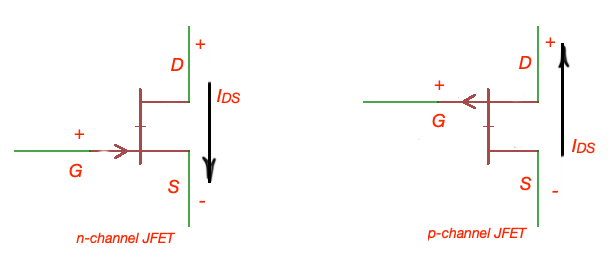
JFET transistor is a three-terminal device, where one of the terminal can control current between two others. JFET transistor terminals are drain (D), source (S) and gate (G). Here current between D and S can be controlled by gate-source voltage.

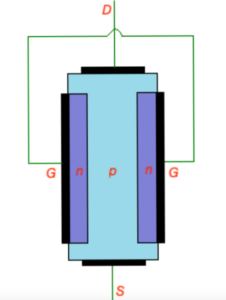
Construction of JFET transistor is depicted on the figure below. N-type JFET transistor consist of n-type semiconductor with heavily doped p-type regions as shown on the figure. P-type areas are forming the gate, both p-type areas and n-type area are equipped with thin contacts layers.

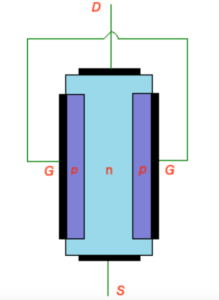
JFET n-type

JFET p-type

JFET electrical symbols

Let’s consider n-type JFET transistor. Here n-type semiconductor is connected to drain and source with ohmic contacts, p-type semiconductors are connected to the gate and connected to each other.

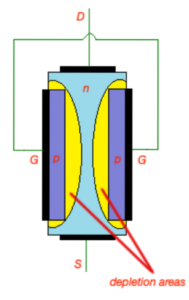
JFET transistor is in cut-off mode, and does not conduct any current when both source-gate and drain-source potentials are zero. There is thin depletion regions are formed around p-type regions of JFET. Depletion regions are free from free careers, so there is no current through depletion area.

Let’s keep

$v_{GS}=0$

and apply drain-source voltage

$v_{DS}>0$

. Current

$I_D$

will flow from drain and source (note that electrons will move in the opposite direction). Here JFET transistor operates in ohmic mode. Depletion region around p-type areas is wider close to drain because of the voltage distribution  between drain and source. When

$v_{DS}$

is growing, width of depletion areas close of drain is growing as well. At some point drain-source voltage will reach

$v_P$

level, when these depletion areas will get very close to each other.

$v_P$

voltage is called pinch-off voltage. After this point JFET transistor will go to the saturation mode. Here small channel between two depletion areas will still exist with constant current through is

$I_{DSS}$

.

If

$v_{GS}<0$

, depletion regions still grows around p-type areas of JFET transistor. In order to maintain depletion regions

$v_{GS}$

should be smaller than

$v_{DS}$

. Lower

$v_{GS}$

. lower pinch-off voltage

$v_P$

. Finally when

$v_{GS}=–v_P$

,

$I_{DSS}=0$

. JFET is off.

 

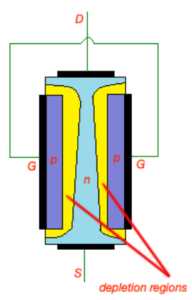Ohmic mode

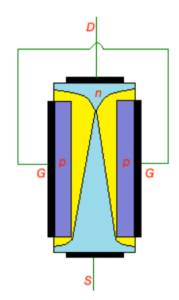
Saturation mode

When JFET transistor operates in ohmic mode, the resistance of n-channel can  be controlled by

$v_{GS}$

voltage, so JFET behaves like a voltage-controlled resistor.  First approximation of JFET resistance in this case is

$r_{DS}=\frac{{v^2}_P}{2I_{DSS}(v_{GS}+V_p{)}^2}$

.

Finally equations, describing JFET transistor behaviour are:

$V_{GS}<–V_p$ $$

for cut-off region;

$v_{DS}>V_{break}$

for breakdown voltage;

$v_{DS }<\frac{v_{GS}+v_p}{4}, v_{GS}>–v_p$

,

$i_D=\frac{i_{DS}}{R_{DS}}$

,

$R_{DS}=\frac{{v_p}^2}{2I_{DsS}(v_{GS}+v_p)}$

for ohmic region;

$i_D=\frac{I_{DSS}}{{v_p}^2}(v_{GS}+v_p{)}^2, v_{DS}>v_{GS}+v_p, v_{GS}>–v_p$ $$

for saturation region. Here

$I_{DSS}$

is a maximum current, when

$v_{GS}=0$

and

$v_{DS}>v_P$

.

If

$v_{GS }< v_P$

,

$I_D=0$

.

If

$0<v_{GS}<v_P$

, then

$0<i<I_{DSS}$

.

JFET transistor transfer function

Transfer characteristic is the relation between output current

$I_D$

and controlling voltage

$V_{GS}$

.  The easiest way to obtain transfer characteristic is to apply Shockley equation

$I_D=I_{DS}(1–\frac{v_{GS}}{v_P}{)}^2=f(v_{GS})$

.  It gives us

$I_D=I_{DSS, }$

when

$v_{GS}=0$

and

$I_D=0$

, when

$v_{GS}=v_p$

. Here we are having  important relationship between

$v_{GS}$

and

$v_P$

is

$v_{GS}=v_P(1–\sqrt{\frac{I_D}{I_{DSS}}})$

.

In order to outline the transfer function, we must calculate

$I_D$

current for different key levels of

$v_{GS}$

.

Transfer function can be obtained from the

$I_D\left(v_{DS}\right)$

characteristics like on the figure below.

Fixed-bias JFET configuration

Three most important relationships for operation of FET transistor devices are

$I_G=0, I_D=I_{S }$

and Shockley equation

$I_D=I_{DSS}(\frac{1–V_{GS}}{v_P}{)}^2$

.

Here

$v_{in}$

and

$v_{out}$

are ac levels.

 

$v_{DS}=v_{DD}–I_D{R}_D$

,

$v_G=v_{GS}$

,

$v_D=v_{DS}$

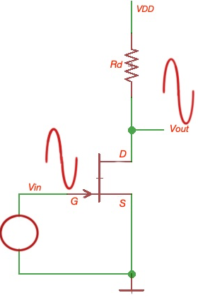
, because

$v_S=0V$

.

$I_D=I_{DSS}(1–\frac{v_{GS}}{v_P}{)}^2$

.

Self-biased JFET transistor configuration

 

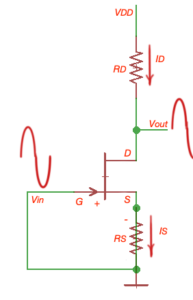
Here

$v_{RS}=–v_{GS}$

, and from the other side

$v_{RS}=I_S{R}_S$

,

$I_D=I_S$

then

$v_{GS}=–I_D{R}_S$

and

$v_{DS}=v_{DD}–I_D{R}_S–I_D{R}_D$

.

$v_G=0, v_S=I_D{R}_S, and v_D=V_{DD}+I_D{R}_S$

,

In accordance to Shockley equation

$I_D=I_{DSS}(1+\frac{I_D{R}_S}{v_P}{)}^2$

, then we are having second order equation that will lead us to quadratic function.