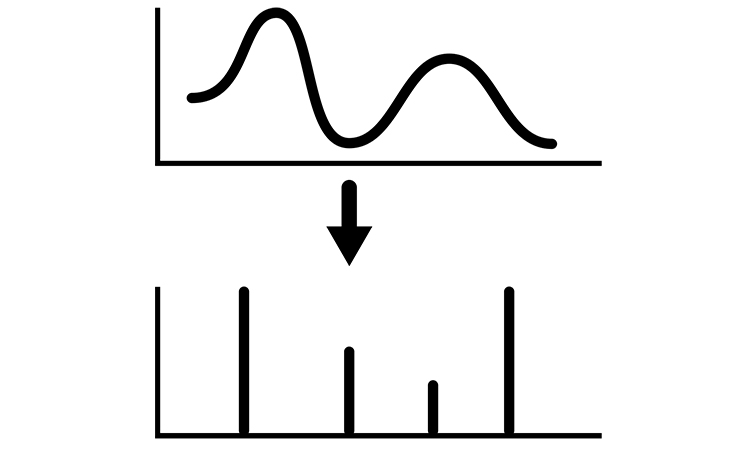
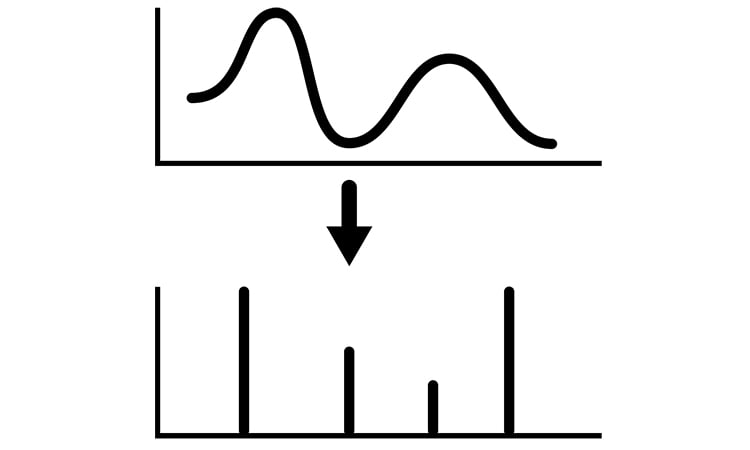
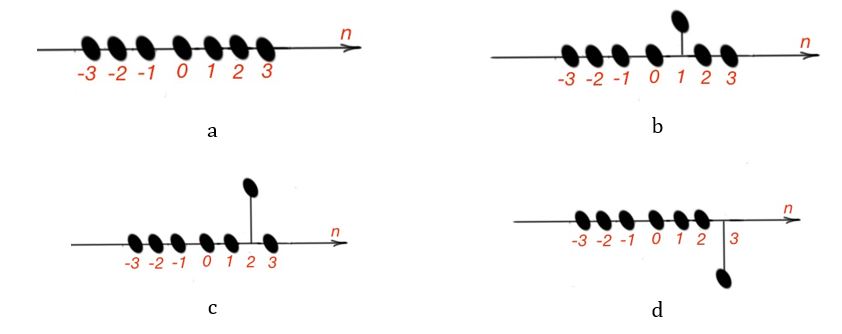
This post answers the question “What is discrete LTI system?”. It is useful to consider discrete-time signals as a sequence of impulses. For example, a discrete-time signal is on show in Figure 1. Figure 2 shows its mathematical representation, where the signal is divided into the single impulses. S, the sum of these individual impulses, form the initial discrete-time signal.
The sum of the impulses is:
. In the other words the discrete-time signal is the linear combination of shifted impulses
with the weight
. This equation is called the shifting property of the discrete-time unit impulse.
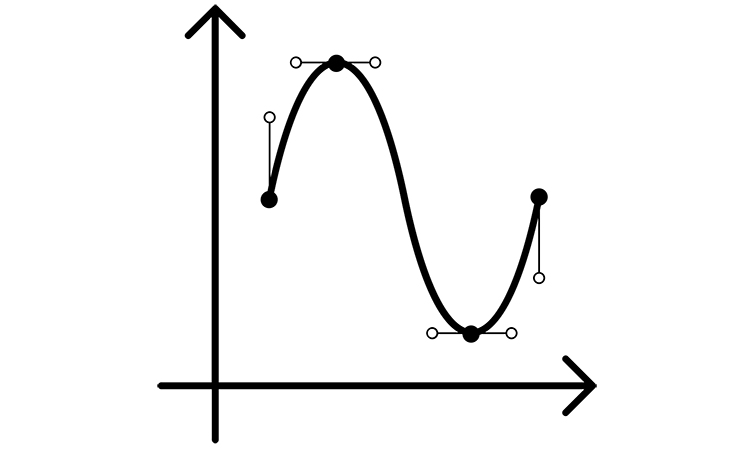
![The mathematical representation of the discrete-time function x[n].](https://www.electronicspecifier.com/wp-content/uploads/2025/11/figure1-8.jpg)
is a linear time-invariant function, then the convolution sum
is a linear time-invariant function too.
Let’s consider the response of a linear discrete-time function x[n], that can be represented by the sum of impulses
, i.e. a linear combination of weighted shifted impulses.
If the input of the linear system is
, then the output
. Here the
are the responses to the signals .
Generally speaking, the functions
are not related to each other for each particular
. In our case is a response of impulse function, then
is a linear shifted version of itself.
So
. Let’s assume that
.
is the output for the input
of the LTI system. So we have
. This equation is called superposition (convolution) sum of the sequences
and
. Symbolically superposition(convolution) function is represented by
.
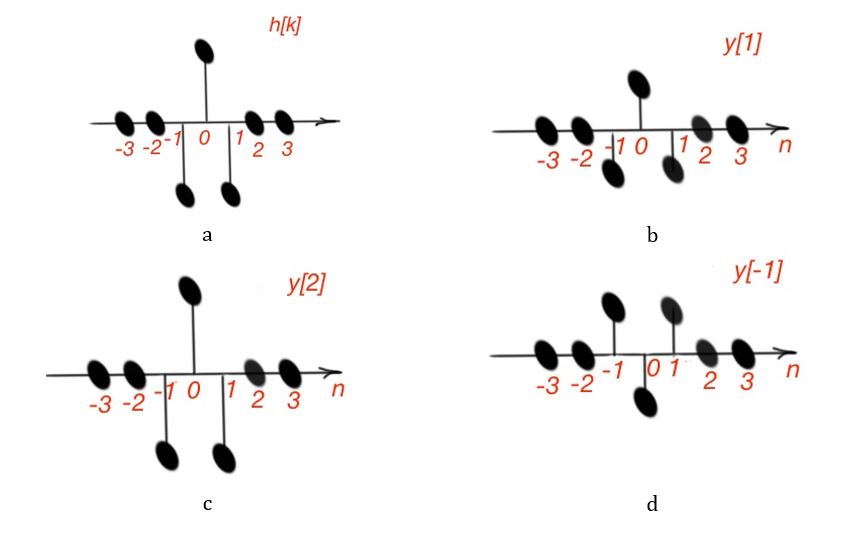
, where
is a response of the impulse
, we have to make the following actions:
1. Determine the function
;
2. Determine the function
.
More educational tutorials can be accessed via Reddit community r/ElectronicsEasy.